Volume 1, Year 2014 - Pages 1-7
DOI: 10.11159/jbeb.2014.001
Pulsatile Aortic Pressure-Flow Analysis using Fractional Calculus for Minimally-invasive Applications
Glen Atlas1,2, Sunil Dhar3, John K-J. Li4,5
1Rutgers New Jersey Medical School, Dept. of Anesthesiology, Newark, New Jersey, USA, 07039
atlasgm@njms.rutgers.edu
2Stevens Institute of Technology, Dept. of Chemistry, Chemical Biology, and Biomedical Engineering, Hoboken, New Jersey, USA, 07030
3New Jersey Institute of Technology, Dept. of Mathematical Sciences, Newark, New Jersey, USA, 07102
4Rutgers University, Department of Biomedical Engineering, Piscataway, New Jersey 08854, USA
5College of Biomedical Engineering and Instrument Science, Zhejiang University, Hangzhou, China
Abstract - Time-dependent
pulsatile pressure and flow waveforms in the aorta carry with them considerable
information regarding the underlying dynamic behavior of the cardiovascular
system. The aortic pressure-flow relationship has traditionally been described
using integer calculus. As such, periodicity and linear system assumptions are necessarily
imposed to extract hemodynamic information. We introduce the use of fractional
calculus (FC) to relate minimally-invasive measurements, of the velocity of
aortic blood flow with an esophageal Doppler monitor, to the derived aortic
pressure. The basis for this research is a Taylor series model of the velocity
of aortic blood flow with subsequent term-by-term fractional integration as
well as fractional differentiation. These results demonstrate that this FC
approach could potentially generate the aortic pressure waveform throughout
systole. Further studies of its first derivative, or the time rate of pressure
change, 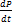 , may also allow its maximal value,
, may also allow its maximal value, 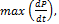 to be computed for use as an index of left
ventricle contractility when noninvasive ultrasound Doppler flow velocity is
available in the clinical setting.
to be computed for use as an index of left
ventricle contractility when noninvasive ultrasound Doppler flow velocity is
available in the clinical setting.
Keywords: Fractional calculus, Aortic blood flow, Esophageal Doppler monitor, Differintegral, Differintegration.
© Copyright 2014 Authors - This is an Open Access article published under the Creative Commons Attribution License terms. Unrestricted use, distribution, and reproduction in any medium are permitted, provided the original work is properly cited.
Date Received: 2014-08-21
Date Accepted: 2014-12-12
Date Published: 2014-12-15
1. Introduction
Hemodynamic diagnosis and clinical management often focus on blood pressure and flow measurements and subsequent analysis of their temporal relationship [1]. Routine catheterization can readily provide left ventricular pressure and aortic pressure, as well as cardiac output, from thermodilution. However, beat-to-beat flow measurements are less common. On the other hand, ultrasound Doppler echocardiography can provide images of cardiac and large vessel structures as well as blood flow velocity. Nonetheless, the aortic blood pressure waveform cannot be obtained.
Noninvasive or minimally-invasive approaches are preferred methods for routine clinical diagnosis and follow-up. Tonometer-based measurements, of blood pressure overlying the carotid artery, have been common [2], but are much less frequently used in conjunction with Doppler ultrasound in the clinical setting. It is possible to derive central aortic pressure when the Doppler ultrasound aortic flow velocity is known [3], [4]. These latter traditional hemodynamic models are typically based upon a linear second-order system utilizing the acceleration, velocity, and displacement of blood flow [5]. By convention, acceleration is defined as the first derivative of velocity, with respect to time, whereas displacement is its indefinite integral. In contradistinction, fractional calculus (FC) is based upon both integer and non-integer differentiation as well as integer and non-integer integration [6], [7].
2. Related Work
FC, although three centuries-old, has recently found applications in the analysis of biological systems. For instance, Djordjevic et al. [8] developed a rheological model of airway smooth muscle cells using a method incorporating FC and a least-squares data fitting technique. They showed that FC could be effectively utilized to account for a weak power law frequency dependence of cell rheological behavior. This effect could not be explained with traditional viscoelastic theory. Recently, an FC dynamic model has been applied to generate electrocardiogram (ECG) signals based upon oscillations and a global optimization scheme. This technique subsequently generates a realistic time series, of the ECG signal, and may find potential applications in modeling abnormal and irregular patterns of cardiac conduction [9].
We have considerable experience with the use of esophageal Doppler monitor (EDM) for minimally-invasive measurement of the aortic flow velocity waveform [5]. This paper provides the first such application of FC to minimally-invasive hemodynamic studies and demonstrates how FC-based modelling could be effectively utilized in understanding the aortic pressure-flow relationship during systole.
3. Methods
3.1. Fractional Calculus
To cognize this application of FC, traditional integer differentiation is first examined for a power function of time:
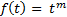 .
.
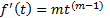 .
.
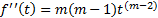 .
.
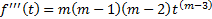 .
.
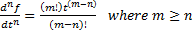 .
.
In a likewise manner, the nth repetitive integer integration process can also be examined for a power function of time:
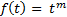 .
.
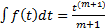 .
.
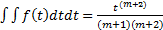 .
.
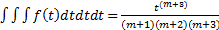 .
.
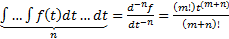 .
.
Note that a constant of integration can be utilized after the completion of the repetitive integration process.Thus, using either (5) or (10), repetitive differentiation or repetitive integration can be similarly accomplished using either positive or negative values for n respectively.
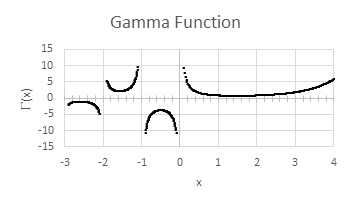
The gamma function 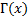 can be defined as [10]:
can be defined as [10]:
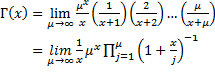 .
.
Note that the gamma function is not defined for values of x equal to either zero or negative integer values. Furthermore, when x is a positive integer, the gamma function has the following property:
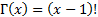 .
.
Additionally, 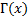 "smoothly connects" the integer values of the
factorial function. It is therefore suitable for defining non-integer
factorial values. The gamma function is illustrated in Figure 1.
"smoothly connects" the integer values of the
factorial function. It is therefore suitable for defining non-integer
factorial values. The gamma function is illustrated in Figure 1.
Equations (5) and (10) can then be modified to utilize the gamma function:
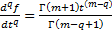 .
.
Equation (13) can be used as the definition of the differintegral [11]. Where q can have a positive value; either integer or non-integer.1,2 Note that q can also take on integer or non-integer negative values:3sup>
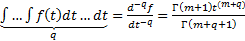
The term q is referred to as the order
of differintegration [12]. Additionally, 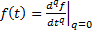 . As previously stated, G(0) is not defined. The
gamma function is also not defined for negative integer values. Thus, specific
fractional derivatives, or fractional integrals, may be unattainable.
. As previously stated, G(0) is not defined. The
gamma function is also not defined for negative integer values. Thus, specific
fractional derivatives, or fractional integrals, may be unattainable.
Owing to either the positive or negative value of q in (13), the differintegral can therefore be utilized for the fractional differentiation, or fractional integration, of power functions. Furthermore, using FC, differentiation and integration may possibly be represented as a continuous process rather than discrete processes.
3.2. Fractional Calculus and the Taylor Series of an Exponential Function
The Taylor series for an exponential function is:
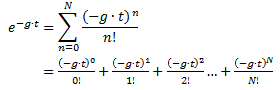 .
.
Thus, for a sufficiently
large N, an exponential function can be accurately approximated as a
summation of power functions. Using the above methodology, the Taylor series
for an exponential can therefore be term-by-term fractionally differentiated or
fractionally integrated:
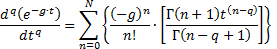 .
.
For mathematical purposes, t cannot equal zero and be raised to a negative power. However, t can take on positive near-zero values. Negative values of t can also yield complex results. To further reiterate, care must be used when selecting integer values of q to prevent undefined values of the gamma function from occurring
4. Examining the Velocity of Aortic Blood Flow
The esophageal Doppler monitor (EDM) is frequently utilized to assess the velocity of aortic blood flow during systole. The EDM allows clinicians to accurately assess patients' cardiac output and stroke volume during anesthesia and critical care conditions [13]. Figure 2 illustrates this waveform.
This velocity, v(t), can be modelled as [5]:
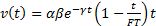
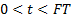 .
.
Where a represents an acceleration term and b is a dimensionless gain. The time spent in systole is referred to as flow time, FT. It should be noted that g can be determined [5]:
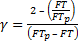
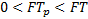 .
.
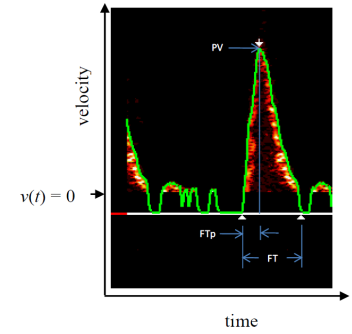
Note that FTp represents the time at which peak velocity (PV) occurs. This is illustrated in Figure 2. Using a Taylor series, v(t) can subsequently be approximated as a time-based power function:
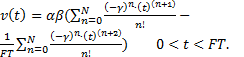
By means of the aforementioned technique, fractional derivatives and fractional integrals of v(t) can then be determined:
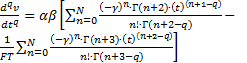
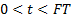 .
.
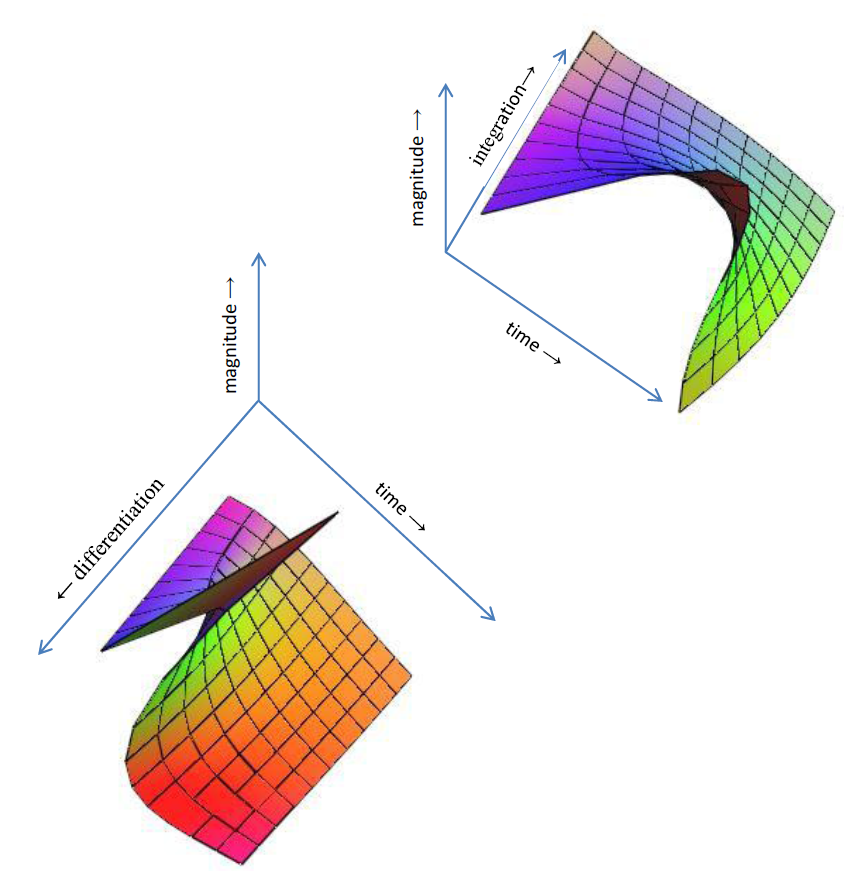
Figure 3 demonstrates the continuous
differintegral (20) over the range: 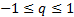 .
.
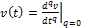
5. Numerical Assessment
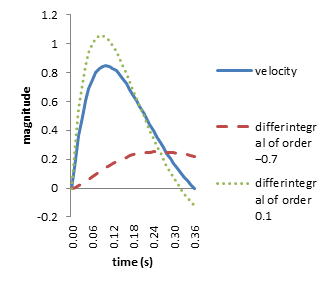
Using MATHCAD (PTC Corp., Needham, MA, USA) v(t) can be calculated utilizing the numerical values from Table 1. Subsequently, its differintegrals of order −0.7 and 0.1 can both be determined. These functions are illustrated in Figure 4.
Note that the dimension
associated with v(t) is m/s whereas that of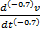 is m/s(−0.7).4
Furthermore, the dimension of
is m/s(−0.7).4
Furthermore, the dimension of 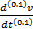 is m/s0.1.
is m/s0.1.
Table 1. Numerical values used for initial computational purposes
| Term | Value | Units | Notes |
| α | 7.25 | m/s2 | acceleration |
| β | 3.00 | dimensionless | gain |
| γ | 6.154 | s-1 | exponential decay |
| FT | 0.36 | s | flow time |
| FTp | 0.1 | s | time to peak flow |
| a | -0.7 | dimensionless | order of fractional differintegration |
| b | 0.1 | dimensionless | order of fractional differintegration |
6. The Systolic Pressure-Flow Relationship in the Aorta
Using (20), a straightforward model of aortic blood pressure, P(t), as a function of the velocity of aortic blood flow during systole is:
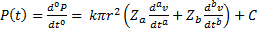 .
.
Where r represents the radius of the aorta, and a and b are both velocity-based differintegrals of order −0.7 and 0.1 respectively. The term Za is "reactance-like" and would be analogous to a combination of elastance and resistance. Whereas Zb would be analogous to a combination of inertia and resistance. Furthermore, C is a constant of integration and k converts units of Pascals to mmHg. In addition:
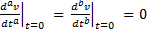 .
.
So that C also functions as an initial condition. Moreover, for the purposes of this preliminary assessment, a "trial and error" technique was employed to determine numerical values for a, b and Za and Zb. These are displayed in Table 2. Note that Za and Zb have magnitudes which are "ballpark approximate" to those of traditionally-derived resistance, elastance, and inertia.
The above model can also
be utilized to assess 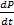 during systole:
during systole:
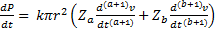 .
.
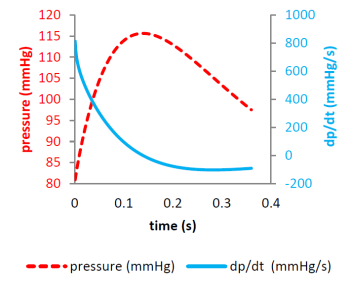
Both P(t)
and 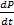 are illustrated in Figure 5. Note that a positive
near-zero initial value for t, instead of zero, has to be used in (23)
to prevent a "division by zero" singularity error from occurring.
are illustrated in Figure 5. Note that a positive
near-zero initial value for t, instead of zero, has to be used in (23)
to prevent a "division by zero" singularity error from occurring.
Table 2. Numerical values used for final computational purposes
| Term | Value | Units | Notes |
| C | 80 | mmHg | constant of integration |
| k | 0.0075 | mmHg/Pascal | unit conversion |
| r | 0.011 | m | aortic radius |
| Za | 3.157•107 | N•sa/m5 | "reactance-like" term |
| Zb | 7.015•106 | N•sb/m5 | "reactance-like" term |
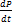 is also displayed
is also displayedStraightforward linear algebraic techniques could also be applied. This would allow "real-time" or beat-to-beat assessment of the "reactance-like" terms, Za and Zb. The following matrix relationship is derived using (21):
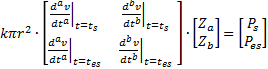 .
.
Thus:
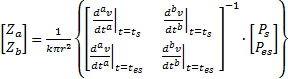 .
.
6. Discussion and Conclusion
Noninvasive assessment, of the hemodynamics within large arteries such as the aorta, has been limited, although invasive means have been commonplace in the clinical setting through catheterization [1], [14]. Advanced imaging modalities can provide geometric and detailed structural changes, but the dynamic properties of the pressure-flow relationship is typically not obtainable. Esophageal Doppler ultrasound measurements, of aortic blood flow velocity, have been demonstrated as a useful minimally-invasive clinical tool [15]. However, central aortic pressure cannot be obtained noninvasively.
Applanation tonometry, applied to peripheral arteries such as the carotid and radial, has been reported for noninvasive monitoring of both pulsatile pressure waveforms and arterial compliance [16]. Subsequently, these recorded peripheral waveforms have also been used to derive central aortic pressure waveforms via a transfer function. Clinically, these have been applied to obtain the augmentation index [17] and to assess vascular stiffness. But the temporal aspects, of the aortic pressure-flow relationship through minimally-invasive means, has yet to be demonstrated.
We have introduced a technique, based on FC, for potentially deriving the temporal relationship of aortic pressure and flow throughout systole. The minimally-invasive measurement of the velocity of aortic blood flow is accomplished with an EDM; although this can also be obtained with a transthoracic Doppler echocardiographic monitor; which is commonly utilized in many clinics.
Our approach is novel in that the Taylor series expansion of an exponential function was applied to allow term-by-term fractional differentiation and fractional integration. A closely related work using FC was performed by Craiem and Armentaro [18] who examined the power-law stress-strain relationship within sheep aorta; through simultaneous measurements of pulsatile aortic pressure and diameter. They were able to account for a dynamic frequency-dependent elastic modulus [19].
The rate of rise of aortic
pressure 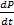 and flow velocity
and flow velocity 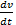 both have a close relationship with myocardial
performance; particularly their peak values,
both have a close relationship with myocardial
performance; particularly their peak values, 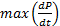 and
and 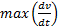 [20]. Thus, the minimally-invasive assessment of
left ventricle contractility is potentially possible using an FC model.
[20]. Thus, the minimally-invasive assessment of
left ventricle contractility is potentially possible using an FC model.
References
[1] J. K-J. Li, The Arterial Circulation: Physical Principles and Clinical Applications, Totowa, NJ, USA: Humana Press, 2000. View Book
[2] J. K-J. Li, Dynamics of the Vascular System, Singapore: World Scientific Publishing, 2004. View Book
[3] C. Bowman, W-M. Shi, and J. K-J. Li, "A new noninvasive method to obtain blood pressure waveforms," Proceedings of the 11th Annual Northeast Bioengineering Conference, 1985.
[4] M. K. Tangella, C. Bowman, J. K-J. Li, "Noninvasive analog measurements of ventricular ejection pressure," Proceedings of the 14th Annual Northeast Bioengineering Conference, pp. 163-165, 1988. View Article
[5] G. Atlas, "Development and application of a logistic-based systolic model for hemodynamic measurements using the esophageal Doppler monitor," Cardiovascular Engineering, vol. 8, no. 3, pp. 159-173, 2008. View Article
[6] M. Dalir, M. Bashour, "Applications of fractional calculus," Applied Mathematical Sciences, vol. 4, no. 21, pp. 1021-1032, 2010. View Article
[7] S. A. David, J. L. Linares, E. M. J. A. Pallone, "Fractional order calculus: historical apologia, basic concepts and some applications," Revista Brasileira de Ensino de Física, vol. 33, no. 4, pp. 4302-1−4302-7, 2011. View Article
[8] D. J. Djordjevic, J. Jaric, B. Fabry, J. J. Fredberg, D. Stamenovic, "Fractional derivatives embody essential features of cell rheological behavior," Annals of Biomedical Engineering, vol. 31, pp. 692-699, 2003. View Article
[9] S. Das, K. Moharatna, "Fractional dynamical model for the generation of ECG like signals from filtered coupled Van-der Pol oscillators," Computer Methods and Programs in Biomedicine, vol. 112, pp. 490-507, 2013. View Article
[10] J. Bonnar, The Gamma Function, Applied Research Press, 2013. View Book
[11] S. Das, Functional Fractional Calculus, Heidelberg, Germany: Springer-Verlag, 2011. View Book
[12] L. M. B. C. Campos, "On a generalized Mittag-Leffler theorem and implicit differintegration," Society for Industrial and Applied Mathematics (SIAM): Journal on Mathematical Analysis, vol. 20, no. 2, pp. 454-467, 1989. View Article
[13] G. Atlas, D. Brealey, S. Dhar, G. Dikta, M. Singer, "Additional hemodynamic measurements with an esophageal Doppler monitor: a preliminary report of compliance, force, kinetic energy, and afterload in the clinical setting," Journal of Clinical Monitoring and Computing, vol. 26, no. 6, pp. 473-482, 2012. View Article
[14] J. K-J. Li, A. G. W. Van Brummelen, A. Noordergraaf, "Fluid-filled blood-pressure measurement systems," Journal of Applied Physiology, vol. 40, pp. 839- 843, 1976. View Article
[15] G. Atlas, J. K-J. Li, and J. B. Kostis, "A comparison of mathematical models of left ventricular contractility derived from aortic blood flow velocity and acceleration: application to the esophageal Doppler monitor," Biomedical Engineering Letters, vol. 4, pp. 301-315, 2014. View Article
[16] G. Drzewiecki, V. Bansal, J. K-J. Li, "Noninvasive measurement of single artery pressure and compliance using tonometry," Conference Proceedings Association for the Advancement of Medical Instrumentation, vol. 30, 1996.
[17] J. E. Sharman, J. E. Davies, C. Jenkins, T. H. Marwick, "Augmentation index, left ventricular contractility, and wave reflection," Hypertension, vol. 54 pp. 1099-1105, 2009. View Article
[18] D.O. Craiem, R. L. Armentano, "Arterial viscoelasticity: a fractional derivative model," Conference Proceedings IEEE Engineering in Medicine and Biology Society, vol. 1, pp. 1098-1101, 2006. View Article
[19] J. K-J. Li, J. Melbin, A. Riffle, A. Noordergraaf, "Pulse Wave Propagation," Circulation Research, vol. 49, pp. 442-452, 1981. View Article
[20] J. K-J. Li, H. Yamazaki, M. M. Bodenheimer, V. S. Banka, R. H. Helfant, "Myocardial performance assessed by peak derivatives of peripheral pressure and flow pulses," Federation Proceedings, vol. 38, pp. 1449, 1979.
Footnotes
1 However, q cannot take on integer values equal to such quantities as: (m + 1) or (m + 2) or (m + 3), etc.
2 Imaginary and complex values of q can also be utilized. However, these will not be addressed in this introductory paper.
3 Note that an alternative terminology could be that of fractional derivatives and fractional antiderivatives.

