Journal of Biomedical Engineering and Biosciences (JBEB)

ISSN: 2564-4998

1. Introduction

Computational biomechanics is an interdisciplinary field that seamlessly blends engineering, biology, and medicine to comprehend biological structures' mechanical behaviour [1]. Through the utilization of the Computed Tomography (CT)-based Finite Element Model (FEM), significant headway has been achieved in simulating this behaviour. This approach enables researchers to investigate complex interactions within the human body, providing insights into various physiological and pathological processes [2]. By combining computational simulations with experimental data, computational biomechanics plays a crucial role in advancing our understanding of biomechanical phenomena, aiding medical diagnosis, treatment planning, and the design of medical devices. The advantages of such approaches are that they reduce speculation and the risk of human error and minimize variations among individual physicians' abilities. Furthermore, it paves the way for scientists and engineers to do examinations before any in vivo experiment.

Imaging technology has become more widespread across various domains in recent years. The Quantitative Imaging Network (QIN) was established by the US National Cancer Institute in 2008. QIN aims to improve quantitative imaging for personalized therapy and the evaluation of treatment responses. Image processing is widely utilized in various fields, including agriculture, finance, engineering, and medicine. Biomedical imaging, in particular, is critical for diagnosing pulmonary diseases such as chronic obstructive pulmonary disease (COPD), cystic fibrosis, lung cancer, and COVID-19 [3]. Medical image processing is vital for accurate 3D bio-analysis to incorporate realistic geometry. It is an imaging process to create a visual presentation of the interior body organs for 3D printing, analysis, diagnosis, and medical treatments. Medical imaging, including magnetic resonance imaging (MRI), CT, Ultrasound, Positron Emission Tomography, X-Ray etc., is processed into a Digital Imaging and Communications in Medicine (DICOM) standard file format [4]. It is used in biomechanical processes, as well as assisting in medical diagnosis, treatment planning, and the development of medical equipment.

Various biomedical software has been used to create an accurate model, such as Mimics, Slicer 3D, etc [5]–[7]. Moreover, Functional Respiratory Imaging (FRI) is a clinically validated computational workflow with functional data, which can be added to respiratory anatomical images. Starting from the low-dose High-Resolution Computed Tomography (HRCT) scans taken at Functional Residual Capacity (FRC) and Total Lung Capacity (TLC), geometric changes in the airways and the lung lobes during breathing cycles are assessed. Such data can be used in combination with Computational Fluid Dynamics (CFD) simulations.

To transform a medical image into a real solid geometry or a Computer Aided Drawing (CAD), which is necessary for FEM, supplementary software is needed between the medical image software and FEM software. The medical image geometries are created from 2D CT or MRI. Further, they need to be repaired and reconstructed before and after converting 3D geometries because of their complexity.

For 3D biomedical image construction, there are two main valuable software: Meshmixer [8] and FreeCAD [9]. Meshmixer is open-source software that enables users to mix created meshes and effortlessly add surfaces by dragging and dropping meshes onto existing ones. It also allows the edition and manipulation of 3D models. On the other hand, FreeCAD is another open-source 3D parametric modeling software that was primarily developed for mechanical design. However, it can also be used for other purposes where users need precise control over the modeling process. It allows users to create complex 3D models easily and accurately, making it a great option for those who want to create intricate designs.

Respiratory diseases like COPD are a significant global public health concern. It ranked as the second leading cause of death in 1990 and the third in 2019, based on age-standardized death rates [10]. Thanks to the development of technologies and their impact on the medical field, medical imaging, CT, and MRI have provided an opportunity to illustrate realistic lung geometry despite their anatomical complexity. Despite the importance of CT-FEM in biomechanics, the number of studies in this domain remains limited by the used geometry, as given in Table 1. For instance, Nasehi et al. [2] developed the lungs with the trachea, acquired for 10 lung cancer patients by a Philips Brilliance Big Bore CT-simulator by using threshold-based segmentation using ITK-SNAP. The objective of their study was to create and assess a technique for forecasting the movement of the lungs' surface during biomechanical respiration modelling. Gordaliza et al. [11] reported the segmentation of the human lung via CT image. A source chest CT volume did the lung segmentation, started 3D rendering of the air-like structures, and detected by threshold. After the 3D rendering of the preliminary lungs, they were connected with airway segmentation.

A vital solution to mitigate the resonance frequency's puzzling is combining the CT-FEM and High-Frequency Chest Compression (HFCC). This happens when a system can quickly transfer energy between different storage modes, such as the kinetic energy in a simple pendulum [12]. Typically, a system has a main resonance frequency and several harmonic frequencies with decreasing amplitudes as they get farther from the source [13], [14]. It is a crucial factor in physiotherapy studies [15]–[17]. To provide effective and gentle Airway Clearance Therapy (ACT), acoustic devices should be designed with the appropriate resonance frequency of the human thorax. This ensures maximum energy supply with minimal amplitude.

Using CT geometries, the lung modelling, including the soft tissues, rib cage, and scapula started in 2014 by Peng et al. [5]. They generated a 3D model of a human respiratory tract to analyse pneumothorax. Recently, Palnitkar et al. [6] improved the modeled geometry created by Peng et al. [5] by adding the computationally designed airways to simulate the sound wave propagation in the airways, parenchyma, and chest wall under normal and pathological conditions.

In order to obtain precise outcomes from 3D numerical analyses, it is crucial to have precise CT-based geometry, as well as accurate material properties of the respiratory systems [18]. Medical imaging is necessary for optimizing the HFCC in FEM. However, no complete human thorax model CT-FEM is currently available in the literature. Rather than using patient-specific applications, the model is based on a CT scan of an average male patient. This makes the study more general and can provide more dependable and replicable results to enhance the understanding of HFCC. The tracheobronchial region has a structural shape that resembles an upside-down tree. As the branches become thinner in the following generations, they maintain a harmonious flow [19]. Upon closer examination, it becomes evident that determining the precise geometry of airway branches and narrowing is a challenging subject. Therefore, a simplified but validated CT-FEM generation methodology brings a revolutionary advancement to biomechanics and biomedical analysis.

Computational biomechanics is an interdisciplinary field that merges engineering, biology, and medicine to comprehend the mechanical behavior of biological structures. With the help of CT-FEM, researchers have achieved substantial progress in simulating this behavior of realistic geometries. However, the challenge lies in attempting to imitate the hierarchical nature of biomechanical behavior by incorporating various scales, from the cellular level to the entire organ. Therefore, the logical decision-making steps, such as assumptions and methodology, play a crucial role.

In the realm of computational biomechanics, CT-FEM holds excellent promise. Nonetheless, a number of impediments must be addressed to fully realize its potential and limitations for multiple internal organs modeling. To the best of our knowledge, even single organ CT-FEM studies are limited; the most developed and validated CT-FEM multiple internal organs inclusive methodology is provided in this study. One aims to develop a methodology for high-quality and comprehensive simulations of multi-internal organs CT-FEM. Different software is selected for the segmentation, surface reduction, surface mesh generation, and acoustic analysis. Decision-making for each software is also explained in detail. The methodology is applied to the human thorax, which consists of soft tissues, rib cage, scapula, lungs, and trachea. Further, the 3D model is validated against experimental data from the literature. The present methodology contributes the development and the accuracy of target-based multiple organ inclusive studies using realistic 3D CT-FEM. Further, it enables scientists to delve into intricate interactions that occur within the human body, leading to significant breakthroughs in the understanding of physiological and pathological processes. It could create a necessary bridge between engineering and clinician studies.

2. Methodology for CT-FEM

One of the primary challenges encountered within the biomechanics field is the accurate representation of biological tissue's physical properties. These properties can differ significantly between individuals and can also vary depending on the patient conditions. Additionally, integrating different scales, ranging from the cellular level to the whole organ, poses a challenge when attempting to capture the hierarchical nature of biomechanical behaviour. Therefore, a validated developed methodology is crucial for multi-organ CT-FEM.

To create the CT-FEM of the human thorax, the process starts with medical image simulation for soft tissues, rib cage, lungs, trachea, and bronchioles in 3D Slicer, as shown in Figure 1. Then, the surface number is decreased to create fine surface meshes and get a realistic geometry from the image. The surface meshes are used for the generation of high-quality meshes in FEM.

2.1. Segmentation of Internal Organs

User interaction is necessary to accurately segment the internal organs in medical imaging for clinical practice and research [20]. This is necessary for computer vision systems, which separate the image of each organ into distinct classes to make upcoming steps easier [21], [22]. With the integration of up-to-date research tools, 3D Slicer offers a range of interactive and user-friendly tools that can be effectively utilized for this objective. The utilization of numerous CT imaging systems often leads to substantial variations, which can pose significant challenges in multi-center and longitudinal studies [23]. In this study, one uses a high-quality CT model that represents an adult male with specific physical properties: 1.82 m height, 72 kg weight, and 1.02 m chest size [24].

In the segmentation tool, five segments were first created using masking. The threshold values for the mask segment range was selected between -300 HU and 3071 HU to identify human soft tissues, which include muscles, skin, fat, and other internal organs. Other internal organs were assumed as soft tissues to simplify the overall geometry.

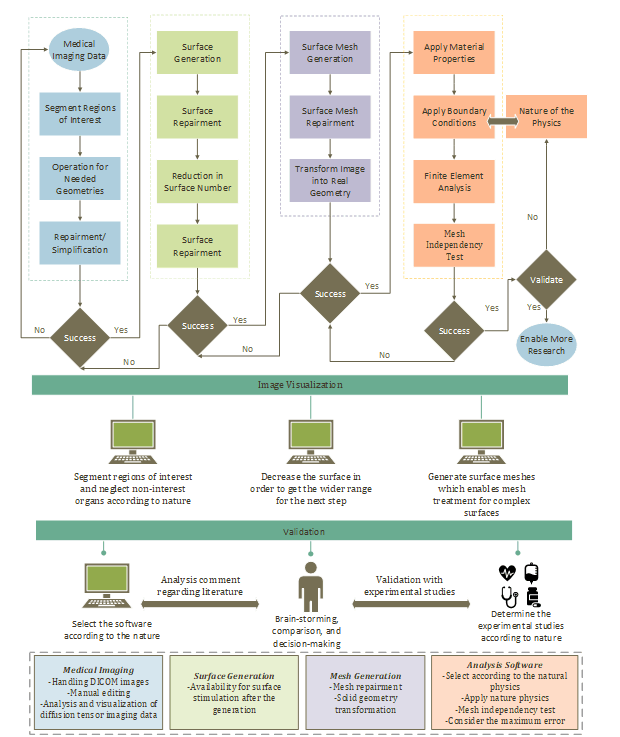
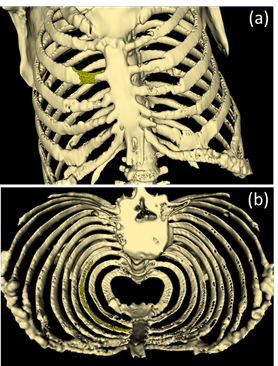
The masking segment was created by isolating certain areas, as open geometries were automatically generated due to the organs present in the torso. Once the exterior spikes have been removed, the interior of the mask becomes completely filled in order to avoid any blank space inside organs for FEM. Median smoothing was applied after these steps to simplify the geometry and remove spikes. Then, the soft tissues were generated by copying the mask segment.

When creating the rib cage, the interior of the soft tissues was selected to avoid double lines in the FEM assembly. The island tool had a threshold range of 135 HU to 3071 HU. After the island progressed, many spikes were detected in the geometries, as shown in Figure 2. As for the repairment of the image, external and internal surfaces were handled carefully.

It is crucial to position the lung geometry properly within the soft tissue environment to prevent double borders and overlapping in FEM. The lungs were generated by slicing the material properties in FEM to remove air, which is assigned as a material property.

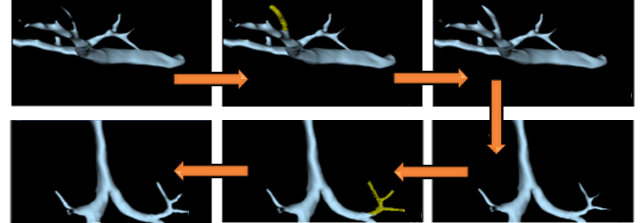
As for the trachea threshold, the range was selected between -3022 HU and -903 HU. During imaging, additional spike geometries were encountered due to the board threshold range of the trachea. These spikes were subsequently removed. Once the borders of the trachea have been determined, the holes are closed to obtain quality meshes in FEM, as illustrated in Figure 3.

During this research, "Segment Editor Extra Effects" extension was used as an essential tool for the segmentation process. To ensure precise outcomes, a combination of manual, semi-automatic, and refinement tools was preferred to construct the complete geometry. Furthermore, one implemented a thresholding range to identify the region based on the Hounsfield units accurately. By using this approach, one was able to achieve accurate and reliable results. Exporting an STL file for the next step is crucial for generating the surfaces and having user interaction.

2.2. Reduction of Surface Numbers

As a first step of the repairment, the geometries of internal organs were separated to make spike geometries more visible and easily detectable. Then the surface number of each organ was reduced to generate surface meshes for simplification and having a good mesh quality in FEM. Having a lot of curvature and spikes in the geometries causes difficulties during the meshing progress.

For the creation of a top-notch mesh for 3D CT-FEM, the number of surfaces has to be minimized while converting surface geometry into a 3D object. The surfaces were repeatedly reduced to ensure the most accurate geometries possible while still maintaining their original form. This was meticulously verified utilizing in analysis software (Figure 1).

2.3. Generating Surface Meshes

Raw unstructured triangulated surfaces in the geometries were created within a standard cartesian coordinate system. In addition to the original function of the software, a selection tool was used to determine the desired surfaces to decrease the number of surface elements.

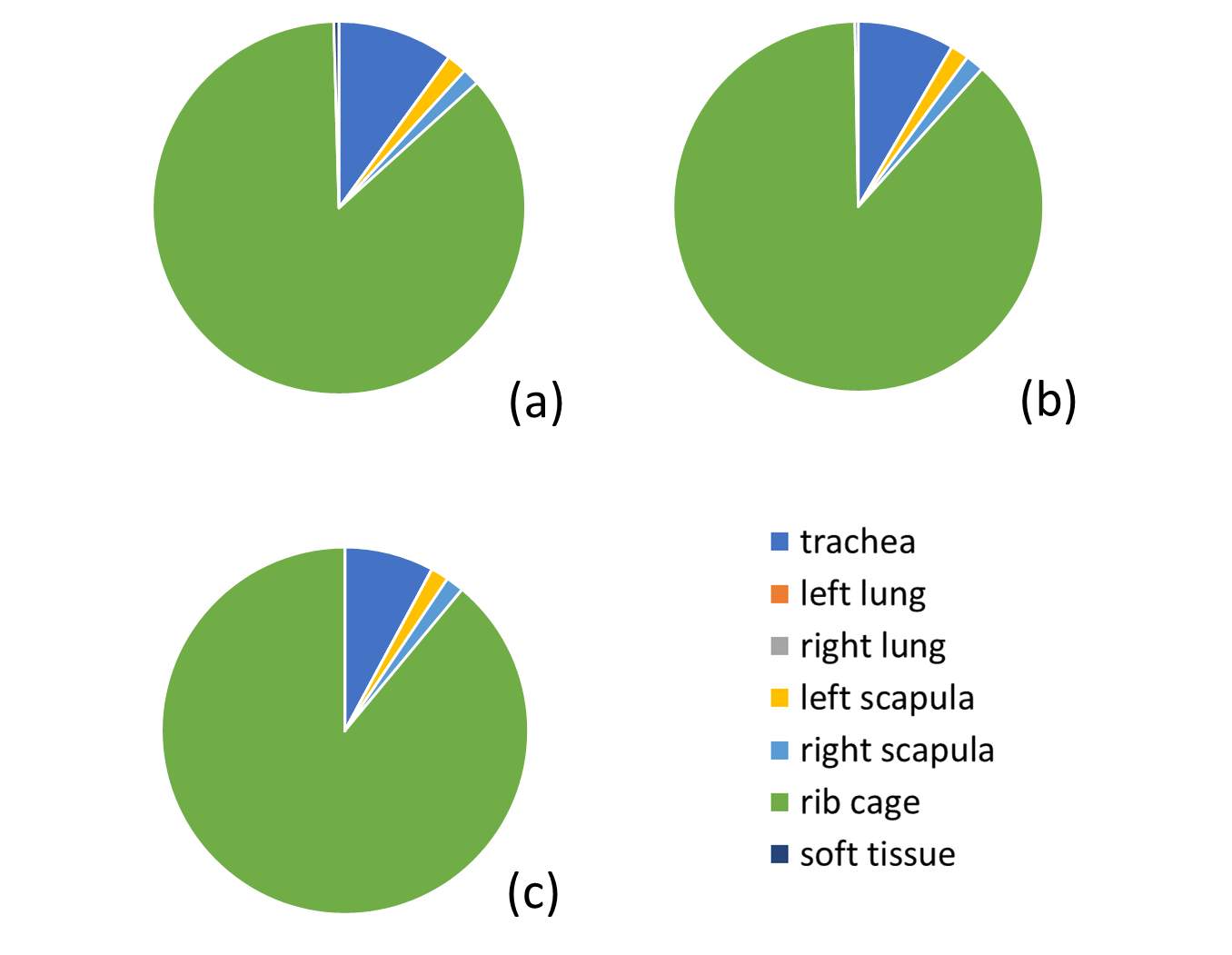
The surface numbers were reduced and surface meshes were created with a tolerance of 0.1 (scale value) when sewing the shape. The surface geometries were then transformed into actual solid geometries, as shown in Figure 5. The created meshes for each human organ were tested, evaluated, and repaired in the software's mesh module. This was done to ensure that there were no issues with orientation, duplicated faces, duplicated points, nonmanifold, degenerated faces, face indices, self-intersections, or folds on the surface. The generated surface numbers, for a total amount of 678 faces, 687 edges and 127 points, were repaired. More than 85 % of repairments were done for the rib cage, the most complex geometry among the internal organs. The second one is the trachea and bronchioles, which comprise approximately 10 % repairments, as illustrated in Figure 4.

The surface and triangular meshes were crafted meticulously for every individual geometry. The resulting human thorax geometry boasted 763k elements, which have been smoothed and optimized for maximum precision.

In pulmonary studies, it is necessary to separate the solid geometry of the mesh for FEM reproducibility and efficiency. The mesh has 8k faces, 13k edges, and 4k points. As expected, the smaller geometry, the trachea, has lower numbers, while the larger, more prominent soft tissues have higher numbers. Repairing the deteriorated meshes in the rib cage geometry was particularly challenging due to numerous spikes and curved geometries.

2.4. Finite Element Analysis

To obtain accurate results, a proper selection of material properties is imperative. In this study, the lung material properties were calculated using Biot's theory [25], while the soft tissues and osseous region properties were extracted from [26], [27].

When considering the human thorax, which consists of 3M tetrahedral elements, 54k triangles, 33k edge elements, and 5k vertex elements, the skewness value is around 0.58.

To conduct studies with external boundary conditions (BCs) applied to the surface of the human chest, it is crucial to model the lungs, airways, soft tissues, and rib cage together. This modeling should align with the physics nature of the validation experimental set-up. It is necessary to accurately simulate the effects of external BCs on the internal organs of humans

It is noteworthy that the numerical tests were conducted within the 20-60 Hz low-frequency range, with boundary conditions fixed according to experiments from [19] and [20].

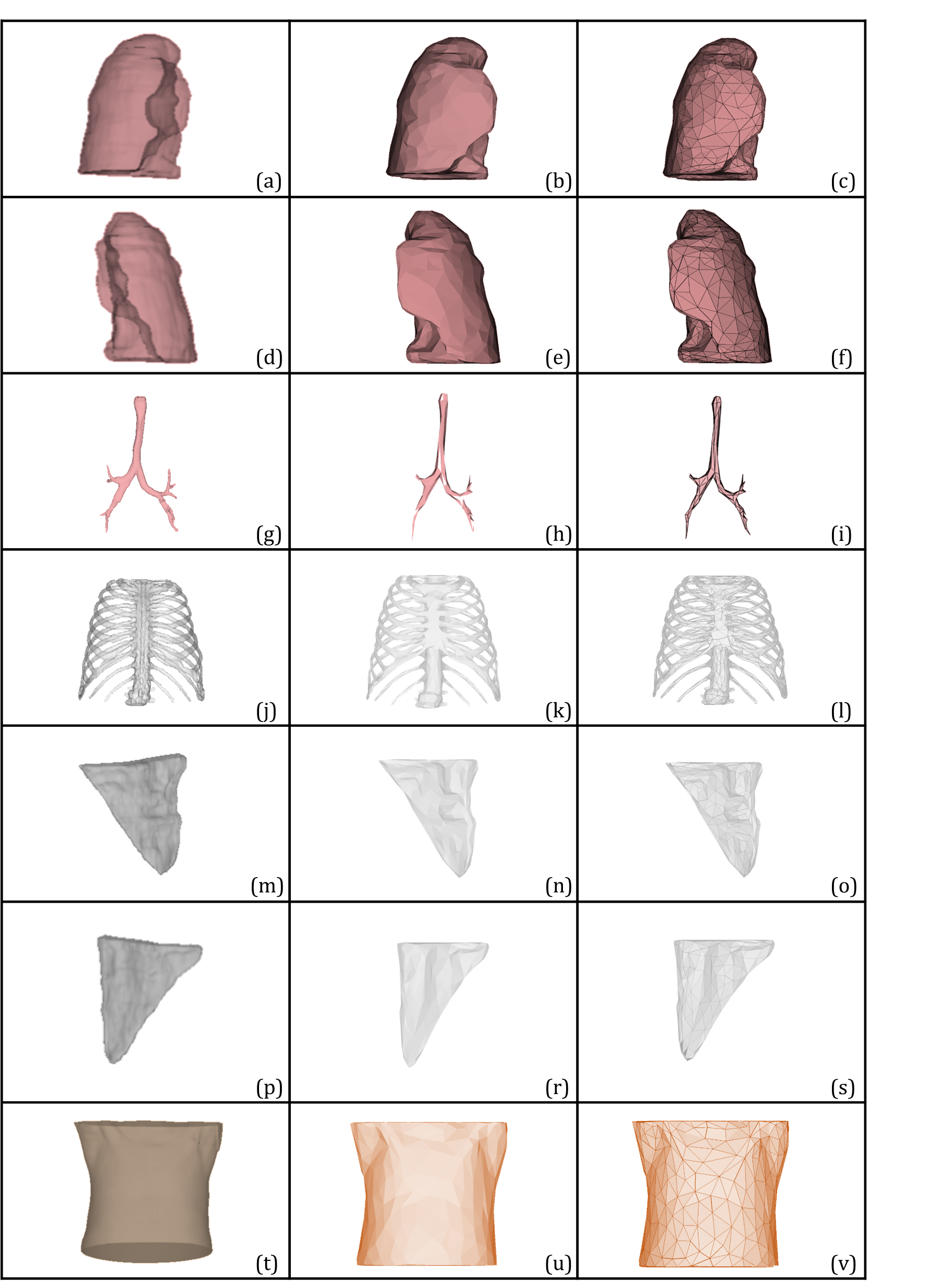
Table1: Comparison between the present generated model and the main models developed within the last 10 years in terms of content and used software.

Year	Geometry Creation	Subject	Content	Developing Software	Reconstruction Software	Ref.
2014	CT	a human	airways	-	ANSYS ICEM CFD	[28]
2014	CT	a pig	lungs and airways	Mimics V14 (Materialise, Plymouth, MI	-	[5]
2014	CT	a pig and a human	lungs, rib cage, and upper torso	Mimics V14	-	[29]
2015	CT	a human	the left lung	-	-	[30]
2016	CT	5 female Landrace and Yorkshire cross pigs	torso, lungs, ribcage, and scapula	Mimics V14	ITK-SNAP	[31]
2016	CT	a human	lungs and trachea	-	CBCT reconstruction techniques	[32]
2016	CT	10 lung cancer patients	lungs and trachea	threshold-based segmentation using ITK-SNAP	-	[2]
2017	CT	a human	oral cavity, oropharynx, larynx and the trachea with three generations of bronchial airways	-	-	[33]
2018	CT	a human	lungs, trachea with three generations of bronchial airways	-	-	[11]
2018	MRI	preterm infants	airways	-	-	[34]
2019	CT	a human	airways	Mimics	SolidWorks	[35]
2020	CT	3 men	torso, lungs, airways (computational), rib cage, and scapula	Mimics V14	ITK-SNAP	[6]
2020	CT	5 healthy and 5 asthmatic humans	airways	-	ANOVA, Matlab for reconstruction	[36]
2023	CT	an adult male (healthy and non-smoking)	fifth-generation of bronchi	Mimics v2s1.0	-	[37]
2023	CT	a male	soft tissues, rib cage, scapula, lungs, trachea, and bronchioles	Slicer 3D	Meshmixer and FreeCAD	*this study

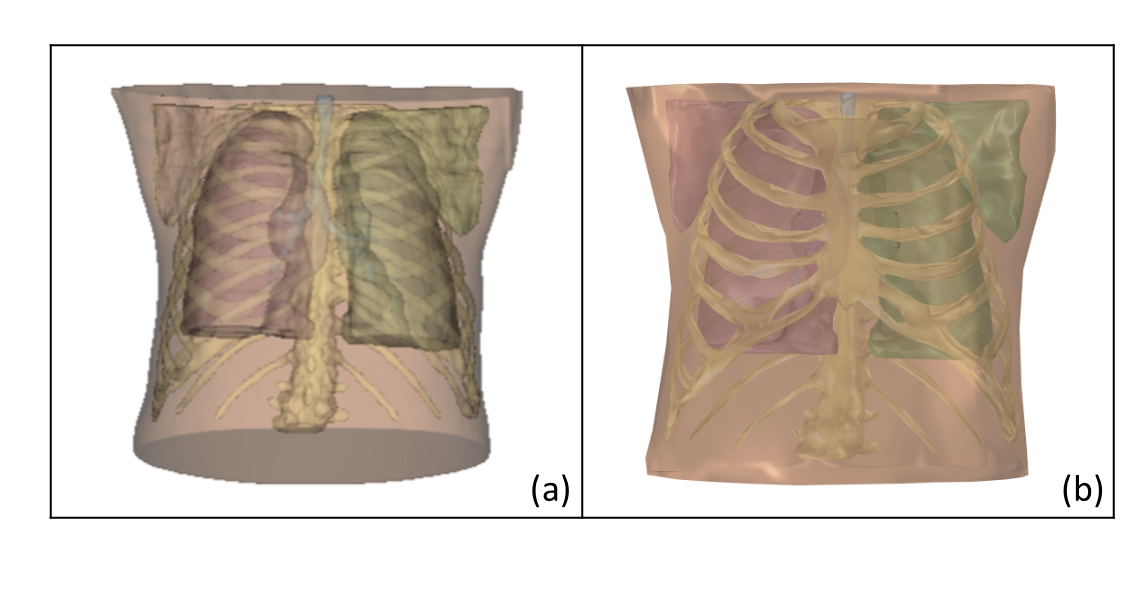
In order to simulate a shaker on the back-chest surface, a cylindrical shape section with a 28 mm radius was utilized. All these details are essential to ensure the reliability and validity of the analysis results.

Ultimately, the process of validation is critical in CT-FEM studies as it not only enhances the reproducibility of the models but also ensures the safety of patients undergoing such analyses. By validating the models, researchers can have greater confidence in the accuracy of their results and the impact of their findings on clinical practice.

3. Model Testing and Validation

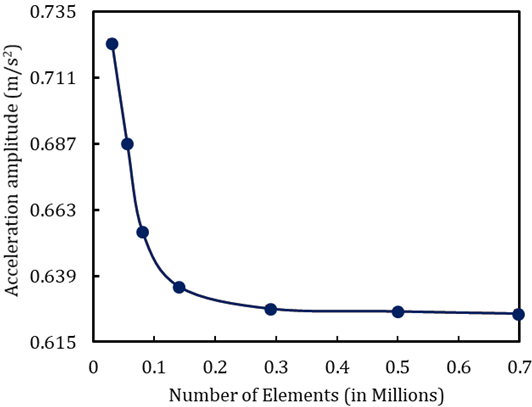
As indicated in Figure 1, a mesh independence test is essential for obtaining precise CT-FEM outcomes. The purpose of this test is to run the model with various meshes, as demonstrated in Figure 7, to determine the optimal element number for the model. We can see the model's sensitivity to the mesh, which converges at 0.3 million elements for both frequency and acceleration amplitude. The errors between 0.3 M and 0.7 M cell elements for frequency and acceleration amplitude are 0 % and 0.3 %, respectively. So the mesh grid with 0.3 M elements has been selected for the study.

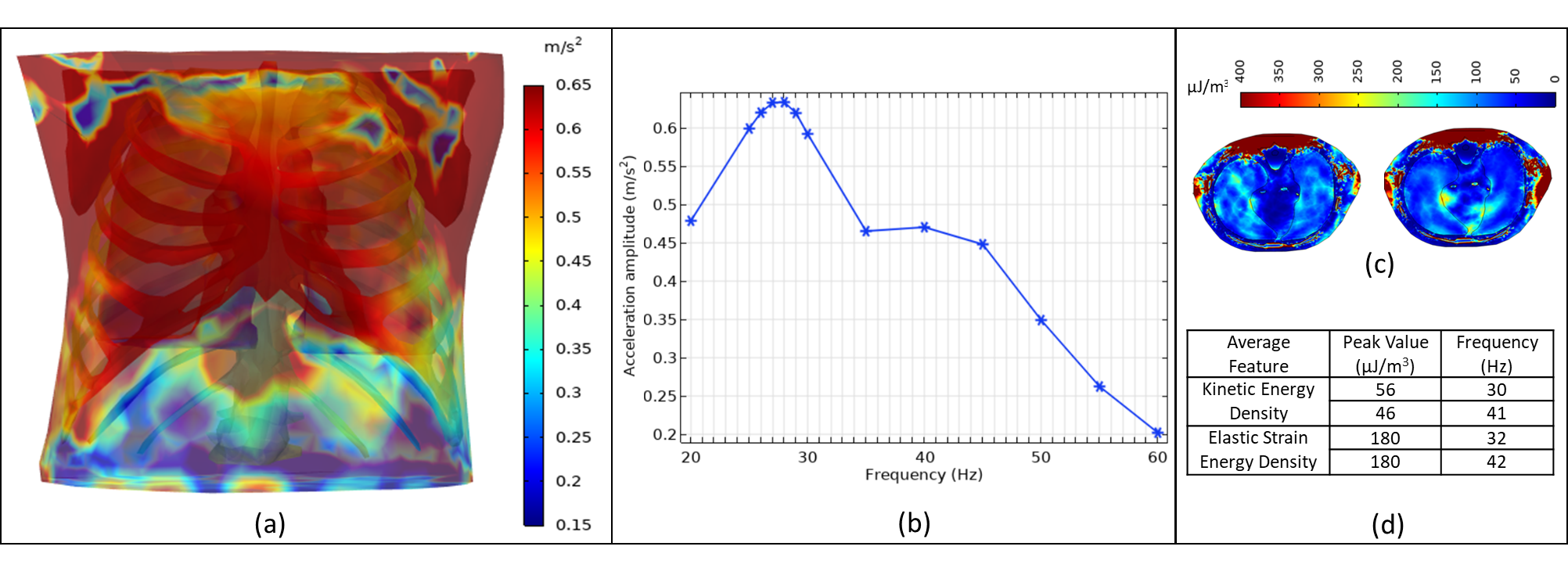
The created realistic high-quality 3D CT-FEM has been already tested for an HFCC treatment numerically and the obtained 3D view of the acceleration amplitude is displayed in Figure 8a. The data obtained at the chest surface lead to a peak value of the acceleration amplitude as 0.63 m/s2 at 28 Hz, as shown in Figure 8b [12]. To ensure accurate analysis and decrease the maximum error, it is crucial to validate the CT-FEM. It will decrease the possibility of errors stemming from the use of various software, numerical schemes, and assumptions.

The realistic 3D CT-FEM agrees particularly well with the experimental results of two independent physiotherapy experimental studies. A notable study by Ong and Ghista [16] on 23 male and female volunteers reported an average peak acceleration of 27 Hz and 28 Hz, respectively. Another study by Goodwin [15] on 15 volunteers found that the resonance frequency differed between males and females, with males showing a resonance frequency of 25 Hz and females showing a resonance frequency of 33 Hz. Based on two independent experimental studies, the current findings support the comprehensive CT-FEM model of the human thorax. This confirms that the generated model [38] is effective in representing the thorax as a whole under the HFCC effect. However, additional analysis is still necessary to examine how HFCC impacts the internal organs, as shown in Figures 8c and 8d [39], [40].

To ensure the accuracy and reliability of CT-FEM, it is essential to validate them through experimental setups that involve either individuals or groups of people, depending on the specific goals of the analysis. To ensure accurate analysis and decrease the error, it is crucial to validate the CT-FEM. It will decrease the possibility of errors stemming from the use of various software, numerical schemes, and assumptions. In order to achieve consistency with finite element analysis, the physics used in the experimental procedures should be carefully selected and applied.

4. Conclusion

CT-FEM of the human thorax appears as a valuable tool for both medicine and biomedical engineers. The intricate interactions within the human body can be thoroughly studied by this method, leading to significant revelations regarding both physiological and pathological processes. Such findings hold immense potential for developing more effective treatments for various chronic respiratory diseases and patient conditions.

In this paper, comprehensive and detailed decision-making criteria and methodology for creating a highly realistic 3D CT-FEM have been developed with an emphasis on the human thorax. However, it is noteworthy that it can be applied to any target-based multiple internal organ regions. The present model included all the necessary multiple organs such as soft tissues, rib cage, bones, lungs, and trachea.

To ensure the accuracy and reliability of the model, one utilized experimentally supported CT-FEM and incorporated detailed explanations of essential mesh quality, computation repairments and simplification methods. After thorough testing using acoustic FEM, the resulting 3D model resulted in a resonance frequency of 28 Hz [12], which aligns with values reported in two experimental physiotherapy studies available in the literature . Therefore, this methodology offers significant potential for improving the efficiency and safety of HFCC therapy, and its effect on the internal organs [39], [40]. Therefore, it is a promising tool for intricating interactions within the human body, leading to significant breakthroughs in understanding physiological and pathological processes. It is a potential bridge between engineering and clinician studies.

In the near future, this 3D CT-FEM methodology could be a promising guide for other studies in creating any target-based multiple organs including realistic biomedical models. In particular, including the heart and its beating cycle, though being challenging, appears as a necessary step towards a more realistic response of the human thorax.

References