Journal of Biomedical Engineering and Biosciences (JBEB)

ISSN: 2564-4998

1. Introduction

The ideal surgical knot should be able to withstand knot failure either via slippage or rupture [1] in vivo for an appropriate period of time to allow the wound to properly heal [2]. During healing, the suture and invariably its weakest component – the surgical knot [3], will be subject to various static and dynamic loads as the subject goes about an everyday routine. In the event a knotted suture is unable to withstand these forces and fails, incisional hernia or surgical wound dehiscence (SWD) may occur [4], which will lead to subsequent complications when the wound is not allowed to heal sufficiently. Therefore, determining the knot with the best integrity and efficiency is critical.

Although previous studies have investigated the effect of suture techniques and materials experimentally, there remains a paucity of consensus in the outcomes. A study by Riboh et al. [2] concluded that surgeon’s knots are stronger than sliding knots. Conversely, Gandini et al. reported that efficiency of the sliding knots over its counterpart. Van Rijssel et al. [5] has argued that even with an additional cross at the base, the surgeon’s knot held no additional strength benefits over the square knot. With respect to suture materials, a similar lack of consensus exists between studies [5, 6]. Despite the numerous studies conducted, none have sought to compare two of the most commonly utilized knots – the two double throws square knot (2DT), commonly known as the surgeon’s knot, and the three single throws square knot (3ST).

Conventionally, the 3ST knot is the preferred knot of choice as it is ostensibly simpler and more commonly accepted, though this is not based on complete scientific data [8]. 2DT surgical knots, on the other hand, seem to offer greater knot security, although it may require a slightly longer construction time. Surgeons typically choose between these two knots based on institutional practice and norms [9] and yet no prior studies have empirically compared the integrity between the two.

To that end, this study aims to investigate and compare the knot integrity between the 2DT and 3ST surgical knots. Specifically, the analysis will focus on the three key aspects: (i) each knot’s vulnerability to slippage via experimental testing, (ii) suture rupture at the knot via computational modelling, and (iii) efficiency in terms of construction time, which is pertinent particularly when multiple sutures are necessary.

2. Methodology

2. 1. Sample Preparation

A single suture material - Polyglactin 910 (Vicryl; Ethicon, Inc) was selected for this study and all sutures were of a 4-0-gauge size, absorbable synthetic and of multifilament structure. 12 knotted suture samples (n=12) were prepared for each of the two surgical knot configurations. To avoid operator influence, all surgical knots were tied by a single surgeon with proper instrumentation. The 2DT surgical knot, otherwise known as the surgeon’s knot, was prepared with a double-wrapped first throw followed by an additional double throw square knot [10] (Figure 1a). The 3ST surgical knot was prepared with two square knots, in which knot base is crossed only once [11] (Figure 1b).

a) b)

Prior to testing, all samples were knotted around a 44.5 mm diameter cylindrical plastic bottle (Figure 2). The construction time taken to tie each surgical knot was recorded and compared between knot configurations. The time was measured starting when the suture was looped on the underside of the cylinder and the surgeon began the first loop and was stopped after the surgeon cut the last knot’s thread.

The tail ends of the knot were cut to a length of 3mm length [12] and knot loops were cut into equal lengths (Figure 3). Standard force was applied to the tail ends of each sample to test for knot slippage as defined by a binary value where a displacement exceeding 1.8 mm would constitute an unstable knot, and vice-versa [9]. The displacement was measured by the change of length from the tail ends to the knot. Any knot deemed unstable based on the condition described above would be excluded from subsequent tensile experimental testing.

2. 2. Experimental Setup

All knots were tested within 12 hours of being tied. Knots that untied before testing were not included in the calculation of the mean maximum tensile load at failure. A tensile testing machine (Criterion 42 Universal testing Machine, MTS, Eden Prairie, MN) with a load cell of 100N (Figure 4) was utilized. The loops ends were clamped between the crosshead grips with a non-harsh adhesive applied on their inner surface. The grips were mechanically tightened with the use of a hex key to minimize slip during testing. To prevent possible damage to the suture samples, the investigator was careful to not exert excessive force whilst tightening. The distance between grips was adjusted to 90 mm - when the suture was just taut.

The knots were then loaded via a crosshead movement rate of 1mm/s throughout the test until knot failure, either by suture rupture at the knot or knot slippage – wherein a knot completely unravels under tensile loads. Force and displacement values were continuously recorded at a sampling data rate of 10Hz. The mode of failure and maximum tensile load at failure were recorded, and the values compared between the two different suture knot configurations.

2. 3. Statistical Analysis

Statistical analyses were performed in Minitab 19 Statistical Software (2020, State College, PA: Minitab, Inc) which ensured that the data points collected for failure load via slippage and knot construction time conformed to a normal distribution via the Kolmogorov and Smirnov test. Unpaired, parametric student’s t-tests were performed on the data sets to identify any significant differences between the two knot configurations. A P-value < 0.05 was considered statistically significant.

2. 4. Finite Element Analysis

In order to test knot strength with no knot slippage, under the expert guidance of an experienced plastic surgeon, 3D computational models of the 2DT and 3ST surgical knots were drawn within a computer-aided design (CAD) software Solidworks (2019, Dassualt Systèmes Technologies, Providence, RI). Due to the morphological complexity of the knots and to allow for efficient computational convergence, as a preliminary measure, the suture diameter was scaled up to 2.5 mm from the original 0.15 mm diameter of the Polyglactin 910 (Vicryl; Ethicon, Inc), 4-0-gauge sutures. All other measurements in the models were scaled accordingly. Hence, the analysis of the finite element results will focus on the relativity of the values and not the absolute values.

As the computational models are idealized, no external factors concerning angle of pull by the surgeon or force differences corresponding to suture lengths was involved. Therefore, only the knot itself needed to be modelled (Figure 5), resulting in a computationally efficient analysis due to a decreased number of elements within the model. Additionally, the volume of the each knot was recorded.

The 3D models of the knots were then exported to a finite element analysis (FEA) software, ABAQUS (v6.17, Dassualt Systèmes Technologies, Providence, RI) for simulation configuration. As a first approximation, the suture material was assigned with homogenous, isotropic elastic material properties obtained from CES Edupack 2019 (Granta Design, Cambridge, UK), where the Young’s modulus was assigned a value of 2040 MPa, and a Poisson’s ratio of 0.405. These values were of a similar order to suture properties utilized in previous studies [12, 13].

In an effort to determine the effect of external tensile loads on the knot strength, the bottom end of the suture was assigned a fixed boundary condition, where all degrees of freedom were constrained (Figure 5). The top ends of the suture were then subjected to a static force uniformly distributed over the area. Multiple simulations were conducted to ascertain the tensile force necessary for each knot configurations to reach a yielding value of 55 MPa, as defined by the suture material defined in CES Edupack 2019 (Granta Design, Cambridge, UK). At this yield stress, the suture would be at its elastic limit, thus suggesting impending suture rupture at the knot .

Both surgical knot models were assigned with explicit 4-node linear tetrahedron elements (C3D4). An element seed size of 0.2 was chosen so that the intricate profile of the knots could be accurately meshed without compromising its external morphology. The 2DT and 3ST knot computational models consisted of 580, 612 and 533, 861 elements, respectively.

a) b)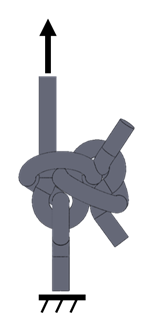

3. Results

In the current study, knot security was evaluated in terms of (i) knot instability prior to mechanical testing, (ii) knot slippage/rupture during testing, and (iii) idealized suture rupture at the knot via finite element modelling.

24 suture samples were evaluated via mechanical tensile experiments. Prior to mechanical testing, two of the 3ST knot exhibited instability, where their displacement values exceed 1.8mm, and were therefore excluded from testing. One 2DT sample was further excluded due to a mechanical testing error during that specific trial. Of the 21 remaining samples, only one 2DT knot sample failed by knot breakage at a tensile load of 13.941 N, while all remaining samples failed by knot slippage. Ultimately, 10 data points were present for each knot configuration that failed via slippage. Due to the lack of data concerning knot rupture, knot failure by slippage will be the primary area of comparison between the two knot configurations. A summary of the number of knots that failed by the various modes are summarized in Table 1.

Table 1. Tally of surgical knots that failed by various modes

Surgical Knot	Two double throws (2DT)	Three single throws (3ST)
Knot instability	-	2
Knot breakage	1	0
Knot slippage	10	10
*Excluded due to testing error	1	-

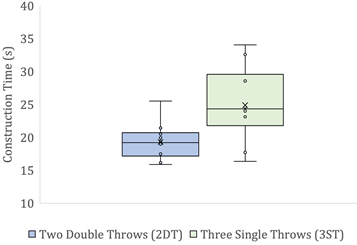
There were significant differences between the construction times (P=0.0153) (Figure 6a) and tensile load to failure via knot slippage (P=5.40× 10^-5) (Figure 6b) between the two knot configurations, where in both cases the P-value fell below 0.05.

a) b)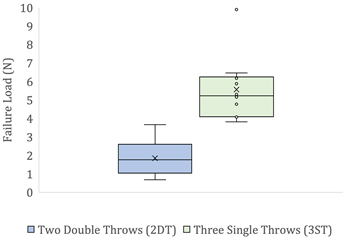

Despite a single outlier value for the 3ST surgical knot failure load, it is evident that in general, the 3ST knot slipped at a higher tensile load, suggesting that it is more resistant to knot slippage. The 2DT surgical knot, however, required a shorter construction time, but slipped at a lower load.

Expectedly, the failure load for suture rupture at the knot of 13.941 N far exceeded the tensile load observed for any failure via knot slippage [12]. However, as there was only a single 2DT knot sample that failed by suture rupture, a comparison between the knot figurations based upon failure by suture rupture could not be investigated. Instead, the computational analyses results, which were a reflection of pure tensile load application and would not mechanically result in any slippage, were then utilized to gain insight into each knot’s vulnerability to suture rupture.

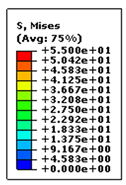
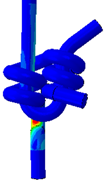
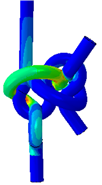
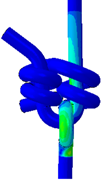
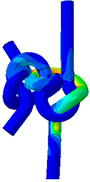
The FEA results revealed that with no possibility of slippage, an applied force of 35.0 N and 16.8 N would elicit a yield stress in a 2DT and a 3ST surgical knot, respectively. The resultant von Mises Stresses in each suture configuration are shown in figure 7. This suggests that assuming no knot slippage, a 3ST knot would first fail by suture rupture at its knot.

		2DT surgical knot	3ST surgical knot
	Front views
	Back Views

Figure 7. Resultant von Mises Stresses in the two double throws (2DT) square surgical knot and the three single throws (3ST) surgical knot. Both the front and back views are shown of each configuration.

Upon preliminary observation, both knots exhibit higher relative stresses at the base of the knot. In the case of the 3ST knot, however, the stresses appear to be concentrated closer to the base, whilst those for the 2DT knot extend further outwards to the exiting strands.

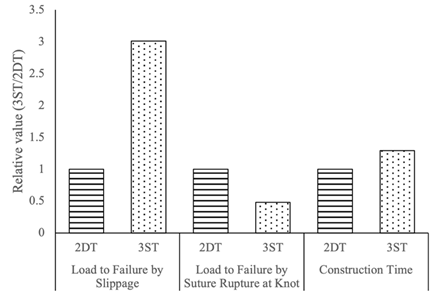
For an efficient comparison, the relevant values for 3ST were expressed as a fraction of the values observed for the 2DT surgical knot. The results are illustrated in figure 8.

4. Discussion

Knot security is one of the most important elements of a tied suture [9]. As a knot is the most vulnerable part of a suture [1,14], it is paramount to ensure that whichever knot is chosen by a surgeon, it remains secure enough to allow the wound to heal sufficiently. Therefore, the objective of the current study is to evaluate two of the most commonly utilized surgical knots – the 2DT or surgeon’s knot, and the 3ST surgical knot on the basis of knot security and construction time.

Through experimental testing and computational analysis, we were able to offer a preliminary comparison between the knot integrity of the two knot configurations. The lower the load at failure, the more vulnerable the knot is to succumb to this mode of failure. The 3ST knot appeared to more resistant to knot slippage with a higher failure load, but more vulnerable to suture rupture when it fails at a value half that of what is required in a 2DT knot (Figure 8), albeit in the idealized case in which a tensile force that is perfectly in line with the longitudinal direction of the suture is applied to its end and slippage does not occur.

The extra throw in the 3ST configuration increases the area of interfacing surfaces, thereby increasing friction within the loop, and possibly leading to its greater resistance to knot slippage. This suggests that the 3ST knot is strong enough to withstand more loads. Therefore, although the current knot has a higher construction time than a 2DT knot (Figure 6a), in instances when surgical wound dehiscence (SWD) via slippage [15] may be life threatening such as in vessel anastomoses, the more time-consuming 3ST surgical knot may be preferred.

The 2DT surgical knot, on the other hand, while more vulnerable to slippage, appears to possess relative acceptable strength, with its yield only initiating at a force double of what is observed in a 3ST knot. Furthermore, the 3ST knot computational stresses are concentrated at the knot base and the extension of stress into the exiting loop strands are relatively shorter than those encountered in the 2DT knot (Figure 7). This may be due to the fact that the 3ST knot configuration reaches its yield at its base much quicker, before the stress could be distributed to the exiting strand. Conversely, in the 2DT computational model, the longer extension of the stresses to the exiting loop strands suggests that the configuration itself may be more efficient at distributing longitudinal loads.

Hence, when a large wound is to be closed that requires multiple sutures [16], the more efficient 2DT that can resist suture rupture better and has adequate strength to withstand more loads may be a suitable option.

Although this study has provided a basis for discussion on the knot integrity of these two commonly performed surgical knots, the result that each knot configuration is vulnerable to a different mode of failure suggests that indeed more research and improvements are necessary to properly determine the biomechanical strength and characteristics of each knot. A larger sample size of sutures, tested between different surgeons where available, may have led to more conclusive observations, specifically with respect to suture rupture. The inclusion of skin tissue samples would have also enabled further study on how each knot configuration affects the skin.

With respect to computational modelling, more realistic and accurate CAD models may be created to include the variation of loop angles within the different knots. In addition, the forces and boundary conditions applied to the computational models were set within an idealized case. In following studies, oblique forces and more specific boundary conditions that control each degree of freedom to more accurately represent in-vivo conditions will be included.

With these improvements, we may gain greater insights relating to the biomechanics of the two knot configurations that could later be used to help guide surgical decisions.

5. Conclusion

In this study, the primary objective was to compare the knot integrity and efficiency between the two most commonly utilized surgical knots – the 2DT and 3ST knots via experimental testing and computational modelling. Although preliminary, the results suggest that that the 2DT knot may be more appropriate in cases where efficiency and resistance to suture rupture is prioritized due to the lower construction time and its higher load at yield. Conversely, where SWD via slippage carries a high risk, the 3ST that is more resistant to slippage is encouraged, despite the additional time required to construct.

Further improvements are necessary to both the experimental and computational aspects of the study to properly determine the biomechanical strength and characteristics of each knot, so that more accurate insights may be revealed that may guide surgical decisions and improve outcomes.

Acknowledgements

The authors wish to thank Johnson & Johnson Pte Ltd for their donation of suture material for the purposes of this study, and Mr Emran Poh from the Singapore Institute of Technology for his help with the illustrations for this paper.

References