Journal of Biomedical Engineering and Biosciences (JBEB)

1. Introduction

Subsidence is a failure mechanism that can occur after implantation of a device. It is defined as the loss of postoperative intervertebral disc height and has been shown to occur in as many as 77% of patients after fusion surgeries [1]. According to actuarial rates subsidence occurs at 63.4 and 70.7 percent at 12 and 16 weeks respectively [1]. Occurrences of subsidence could be due to bone failure, which may be attributed to compressive stresses, or a failure of the implanted device specifically bone graft material [2]. While a loss of height is common, measuring it may be contentious. Identifying the edge of the device proves difficult due to bone in-growth and the shadow of the apophyseal ring. Significant subsidence has been defined differently for the lumbar and cervical regions of the spine. Losses of disc height of 2mm in the lumbar spine and 3mm in the cervical spine have been considered relevant benchmarks [1], [3] and [4]. Another indication of subsidence is the change in lordic curve of the cervical spine. Changes in angle between the endplates, at the surgical level in the case of fusion, would indicate that the device is sinking into the vertebral bodies. Angle changes have been measured at a lordic increase of 1.6 degrees postoperatively to a follow up lordic decrease of 2.5 degrees [4]. The reduction in angle indicates that either the anterior or posterior part of the implanted device had subsided into the vertebral body. This failure is also a localized failure that is initiated by high contact forces generated by implanted disc devices.

Understanding the endplate morphology and biomechanics is crucial to the future success of implanted devices. Several studies have been aimed at determining the thickness, strength and density of the vertebral endplates of the cervical spine by directly measuring cadaver specimens. The thickest regions are in the posterior region of the superior endplate and the anterior region of the inferior endplate with the central region being the thinnest area [5], [6] and [7]. Mechanically the thicker regions of the endplate are stronger than thinner areas [8] and [9]. Oxland showed that the thinner, middle lumbar region had a mean failure load between approximately 60-100 N, and increased toward the endplate's periphery, thicker regions, to a load of approximately 175 N [8]. Locations of thicker endplate bone are indicative of other factors that affect the biomechanical quality of the endplate. Density scans of the endplate, as measured by peripheral quantitative computed tomography (pQCT) scans, reveal that the endplate bone is denser in thicker regions [10]. Results show that an increase in bone density from 150 to 375 mg/mm³ equates to a stiffness increase from 100 to approximately 200 N/mm. These same regions, which have a greater density and are thicker, also have an increased mineral deposition than thinner regions of the cervical endplates [11] and [12]. The increased mineral deposits were located in areas of the endplate that typically have the highest indentation test results and therefore higher failure limits [8], [9], [11] and [12].

Causes of subsidence can be modeled using finite element models. Finite element modeling allows the investigation of several parameters, morphological included, that are crucial to the long-term success of intervertebral devices. Frequently theoretical vertebral geometry is constructed from anthropometric data [13], [14] and [15]. The anthropometric data is typically compiled from measurements taken on a large sample group of cadavers. Theoretical models usually assume geometric properties of parameters that are difficult to measure directly and cost effectively, for example cortical shell thickness. Experimental models built from CT's also have material property limitations but are well suited for replicating anthropometric geometry for a single user. In both cases some assumptions need to be made concerning shell thicknesses. Several studies simplify the cortical shell and endplates as a shell with constant or only a slight variation in the endplate. The goal of this study is to determine if an endplate thickness of a half-millimeter is an adequate approximation for the vertebral endplate by comparing endplate stresses.

2. Materials and Methods

A 3-dimensional linear elastic model of the C3 vertebrae was constructed from CT images of a 25-year old female that consisted of the vertebrae's bony structure. MIMICS 13.0 (Materialise, Ann Arbor, Michigan, USA) was used to convert the CT images to a 3-D model. The 3D model was smoothed and meshed using 3-Matic (Materialise, Ann Arbor, Michigan, USA). From 3-Matic an orphan mesh was imported into Abaqus 6.9 (Simula, Providence, Rhode Island, USA) finite element design suite for post-processing. This experiment considers the thickness of the superior vertebral endplate. The superior endplate was modeled in four different ways, labeled Model 1 through Model 4. The first model, Model 1, used a half-millimeter thick approximation for the superior endplate. Model 2 assumes the endplate has been completely removed. The removal was modeled by the actual removal of the shell elements exposing the volume elements of the core. Model 3 had a superior endplate that is divided into three regions [5]. Model 4 had a superior endplate divided into seven regions [6]. Cancellous core and endplate stress values will be collected and compared. The thickness and region distributions are presented in figure 1.

The finite element model was constructed with 60697 tetrahedral elements and 13651 nodes. The cortical shell was created with 4552 offset shell elements, less for the model with the removed endplate. The shells of the inferior endplate and the radial cortical shell were set to a half-millimeter thickness. All cortical bone was modeled using offset shell elements. Figure 1 shows how the endplates were sectioned.

The cartilaginous endplate was not considered in this analysis because it is often removed during surgery and does not contribute significantly to the stiffness of the endplates [14].

Assigned material properties have been previously well documented in literature and are presented in Table 1. Material properties were considered to be homogenous. This is not physiologically accurate. The assumption was made that on the macro level the irregularities would be evenly distributed throughout the material sections and represented by the assigned values. The properties were made continuous from point to point and assigned in a hierarchical structure, which separates different bone categories, i.e. cortical and cancellous, into different material groups. This is clinically relevant since the material property definitions simulate bone's various material distributions and can be adapted to replicate disease or injury. The entire vertebra was broken down into posterior elements, cancellous core, radial cortical shell and the superior and inferior endplates. All elements were assigned linear elastic element types. The cancellous core of the vertebral body was assumed to be anisotropic. The axial direction is the strongest due to the difference in cortical bone structure and alignment in the axial direction along lines of stress [18] and [19].

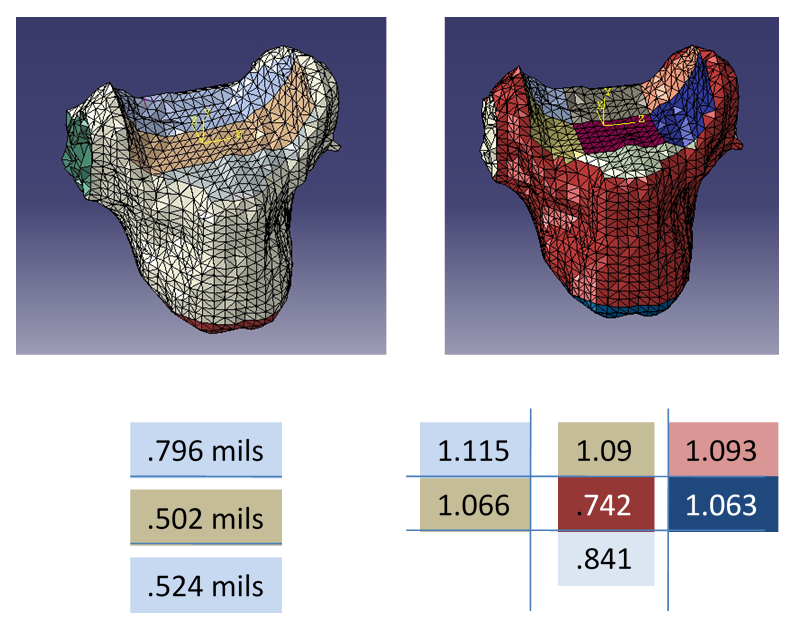
Table 1. List of material properties applied to the finite element model [13], [14], [16] and [17].

	Modulus of Elasticity (MPa)	Poisson's Ratio
Cortical Shell	10,000	0.3
Cancellous Core	Ezz = 344, G1,2 = 63	0.11
	Eyy = 144, G1,3 = 53	0.17
	Exx = 100, G2,3 = 45	0.23
Superior Endplate	1,000	0.3
Inferior Endplate	1,000	0.3
Posterior Elements	3,500	0.25

The models were statically loaded with an axial force of 1000 N in flexion and extension moment of 7.5 Nmm. To avoid the concentration of stress from point loads a pressure distribution was applied to the superior endplate. In this scenario, a higher stress peak develops in the same direction as an applied moment. For example a flexion moment would have a resultant distributed load with a compressive stress peak in the anterior region of the vertebral body. The boundary conditions consisted of fixing the inferior endplate in translation and rotation. These conditions are outlined in Table 2. Magnitudes of von Mises stresses were recorded for each case.

Table 2. List of applied loading conditions.

Condition	Location
Fixed in translation and rotation	Inferior endplate
Axial load of 1000 N in flexion	Superior endplate
Moment of 7.5 Nmm in extension	Superior endplate

3. Results

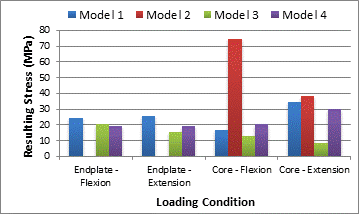
The results show that the endplate stresses are all approximately the same in magnitude and location. The values of stress calculated in this analytical model are presented in the Table 3 and Figure 2. The von Mises stresses range from a minimum of 15.7 MPa, Model 3 in extension, to a maximum of 25.57 MPa, Model 1 in extension. These values are consistent with other studies listed in Table 3. The endplate stresses are also well under the failure stress for cortical bone. The cancellous core stresses are less consistent. A stress range of 8.5 MPa, Model 3 in extension, to 34.5 MPa, Model 1 in extension, was recorded in cases with endplates present. These values are greater than that of the listed failure stress for cancellous bone of 4 MPa, but are in line with some of the previously modeled vertebra in Table 3. In the models with the removed endplate, core stresses reach a maximum of 74.8 MPa, which is much greater than the 4 MPa failure limit.

Table 3. Max stress values observed in the core and the endplate during flexion, extension and axial loading.

Model	Endplate Flexion (MPa)	Endplate Extension (Mpa)	Percent Diff, Model 1 vs. Model 3,4	Core Stress Flexion (Mpa)	Core Stress Extension (Mpa)
1	24.6	25.57	N/A	17.1	34.5
2	N/A	N/A	N/A	74.8	38.2
3	20.7	15.7	17.2, 47.8	13.12	8.5
4	19.5	19.5	22.5, 26.9	20.5	30.14

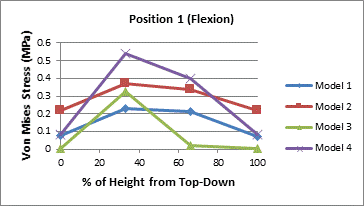
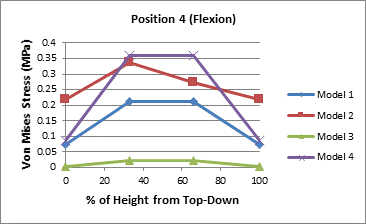
The von Mises stresses were also analyzed at various depths of the vertebral core. This was done to examine how the stress propagated through the cancellous core. Measurements were taken in four spots in the axial plane and at four different depths in the sagittal or coronal plane for a total of sixteen measurements. The locations of the stress chosen in the axial plane were measured where the stress should have been highest in the cases of flexion and extension.

The first set of measurements was taken directly beneath the vertebral endplate. The second set was taken at approximately 1/3 of the height of the vertebral body beneath the superior endplate. The third set was measured at approximately 1/3 of the height of the vertebral body above the inferior endplate. Partial results are presented in the Figure 3 with the complete set of figures in the appendix.

4. Discussion

The stress results from this test were compared to studies conducted examining the stress in the endplate and vertebral body, and the loads used to obtain these stresses. These results are presented in Table 4. Direct comparisons are difficult because of the wide range of loading conditions, vertebral levels, and different study conditions i.e. fusion, curvature and bone grafts. The results of this study are however within these investigated ranges, which suggest the model is representative of the C3 cervical level.

The differences in reported von Mises stresses can be attributed to different loading conditions and boundary conditions among other things. Few studies go into detail about exactly how loads are applied to finite element models or how the models are bounded. Both factors can have large effects on the outcomes of stress maximums. Research has shown that a stress of 4 MPa is the failure limit for trabecular bone and 131-224 MPa for cortical bone [26] and [27]. These limits can be assumed as a benchmark for the onset of bone failure in the endplates and cancellous core.

The stresses developed in this study indicate that a half-millimeter approximation for the vertebral endplate is adequate. The half-millimeter approximation in Model 1 has a maximum/minimum percent difference from the anthropometric models of .478% and .172% respectively (percent differences presented in Table 2). The stress generated in Model 1 is also greater than the other models lending to a conservative design if these values are used for mechanical design considerations. The ability to model the endplate with a constant thickness saves time ultimately making the analysis more efficient.

Table 4. The first listed researcher and the emphasis of the study are in columns one and two. The loading condition is in column three and the stress results in the core and endplate are in columns four and five. The level of the spinal column modeled is in column six.

Study	Subject	Loads	Max Endplate Stress (MPa)	Max Core Stress (MPa)	Study Level
Galbusera et al. [20]	Anterior Cervical Fusion	100 N Axial, 2.5 Nmm Bending	2.80	N/A	C5-C6
Denoziere et al. [15]	Fusion/Mobile Disc	720-1300 N Axial, 11.45 Nmm Axial rotation	90	3.5	L3-L4
Polikeit et al. [13] and [14]	Fusion	1000 N Axial, 12 Nm m Bending	Stress values recorded as percentage increases		L2-L3
Langrana et al. �[21]	Curvatu-re	N/A	40	N/A	L4-L5
Zhang et al. [22]	Bone Filling Material	400 N Axial, 7.5/3.75 Nmm flex, ext	9.503	.584	L1-L2
Zander et al. [23]	Bone Graft Location with Fixators	250 N Axial, 7.5 Nmm flex, ext, lat bend	25	N/A	L2-L5
Dai [24]	Osteopo-rosis	1200 N Axial, 30 Nmm flex, ext	5.17	24.03	Lumbar
Adams et al. [25]	Fusion	1310 N Axial	25	N/A	L5

While the endplate stresses were well under its failure limit of 133 MPa the maximum cancellous core stresses in the Model 2 (removed endplate) were much greater than its failure stress of 2 MPa. For example under flexion the core experienced a maximum stress of 74.8 MPa, which is approximately 35 times its failure limit. Subchondral failure was not investigated in this study so its contribution to failure cannot be addresses at this time.

Von Mises values were also recorded through the height of the vertebral core to examine stress propagation. For all cases the 2 MPa core failure stress was not reached except in the case of Model 1, extension, in the posterior right region of the vertebral body where the stress reached 3.98 MPa. This stress is slightly under the upper failure limit of 4 MPa. Table 5 shows average values for stress in each level of the vertebral body under each loading condition: flexion or extension, while also ignoring Model 2 since it does not have an endplate. Table 6 charts stresses associated with flexion and extension in either the posterior or anterior areas of the vertebral core.

Table 5. Average stress propagation through the vertebral body in flexion and extension.

Height (as percentage from bottom)	Average von Mises Stress in Flexion (MPa)	Average von Mises Stress in Extension (MPa)
100%	0.129	0.900 (0.620)*
66%	0.180	0.561
33%	0.229	0.510
0%	0.054	0.351

*The number in parentheses is not considering the highest possibly outlying stress value.

A general trend, in Figure 3, can be seen that the stress is increases towards the center of the vertebral core. In the upper endplate under extension the trend does not hold even if the highest stressed element is not considered. It's likely that there is some load sharing between the endplate and the vertebral core that redistributes load away from the core at the top and bottom near the endplates. The middle the vertebral body seems sufficiently removed from the endplates thus the higher reported stresses. Table 5 also indicates that the posterior of the vertebral body is stressed higher than the anterior portion under both flexion and extension.

Table 6. Average stress in the posterior or anterior areas of the vertebral body in flexion and extension.

Position	Flexion (MPa)	Extension (MPa)
1,2	0.191	0.691
3,4	0.105	0.467

Removal of the cortical endplate has a significant effect on the cancellous core stress. Ideally the endplate should be left intact as much as possible. From the evidence above the minimum cancellous core stress was 38.2 MPa. This stress is almost 10 times that of failure limit for cancellous bone using a non-conservative failure limit.

This investigation only analyzes a pressure load that is evenly distributed on the vertebral body. Unless a cage or artificial disc fits perfectly in the disc space with continuous contact, stresses will greatly increase at areas of contact [25]. Curvature is particularly important in the cervical spine. Unlike the lumbar region that has large flat endplates the cervical spine has a large curvature in the frontal plane that comes from the uncanate processes [21] and [28].

5. Conclusion

This study shows that a half-millimeter endplate approximation can be used to adequately represent the cortical endplate experimentally. When compared to morphologically complex models the resulting half-millimeter endplate stress was 25.57 MPa and core stresses were 34.5 MPa similar to stresses in other research. It was found that the vertebral body can be modeled analytically without experimentation and can use simplified modeling parameters to save time and cost. Further understanding of regional stress characteristics will be valuable for the design of implantable devices.

This study further provides new understanding of the physiological loading conditions of the C3 vertebrae. These findings will help to improve the design aspects associated with the intervertebral disc design. The design needs to be further improved to reduce the effects of subsidence on the vertebrae and the associated adjacent segment degeneration. Clinical outcome therefore may further be improved along with overall patient satisfaction.

Acknowledgment

The authors would like to thank Miami Valley Hospital (Dayton, OH) for support on this project. Specifically Dr. David Uddin in the Clinical Research Office, Scott Calvin manager of the Miami Valley Imaging Group, and Matt Binkley fourth year medical student, for assistance in collecting CT images.

Conflict of Interest

There are no conflicts of interest in this study.

References