Journal of Biomedical Engineering and Biosciences (JBEB)

1. Introduction and Related Work

Societal lifestyle and occupational trends combined with natural disc degeneration due to aging results in low back pain affecting over 80% of Americans at some point in their lives [1]. The facet joints have been recognized as a potential source of back pain since 1911 [2]. While this incidence rate may be relatively high, perhaps a more pertinent observation involves those individuals who are exposed to elevated frequency loading due to occupation. These include heavy equipment operators, commercial truck drivers and helicopter pilots. A meta-risk analysis for development of low back pain in this population indicated a propensity over twice that of non-operators [3]. In animals, complications due to vibrational loading include compromised nutrition, increased disc pressure, neuropeptide release, and increased creep [4]. Feline models subjected to 60 minutes of cyclic flexion-extension at 40N at 0.25Hz and 0.5Hz respectively, resulted in significant increase in pro-inflammatory cytokines (IL-1β, IL-6, IL-8, TNF-α, TGF-β1) at the higher loading frequency, indicating pronounced changes consistent with an acute inflammation in the supraspinous ligaments of L3-L4 and L5-L6 [5]. In humans, vibrational exposure has been related to low back pain in addition to neck and shoulder pain. [6].

Under certain conditions the effects of high frequency vibration has been shown to provide benefit. Rats bilaterally implanted with hydroxyapatite (HA)-coated titanium in tibiae were treated with low-magnitude high-frequency loading via whole body vibration (VIB) or alendronate (ALN) following ovariectomy. Both the VIB, ALN and sham animals significantly increased bone-to-implant contact, peri-implant bone fraction and biomechanical push out force and interfacial shear strength when compared with the control ovariectomy group. The authors concluded that low-magnitude high-frequency loading enhanced bone-to-implant osseointegration, but the efficacy was weaker than alendronate [7]. Though a number of studies have been conducted to evaluate vibrational transmission to the body, few have focused on isolated spinal structures. One such study by Kaigle et al. investigated the response of porcine intervertebral discs to compressive (100N and 200N) vibrational loading from 0.05Hz to 25Hz. The results showed that dynamic axial stiffness was frequency dependent and increased with successive exposures at the same load magnitude [8].

Finite element analyses have been used extensively to examine the effects upon spinal structures. Using a non-linear finite element model of the L3-L5 spinal segment, Guo et al. examined the frequency effects of axial cyclic loading on the spine. When exposed to long term whole body vibration, the model indicated that the posterior regions of intervertebral disc are more susceptible to injury as compared to anterior regions. Further, the vibrational amplitudes displayed at the facet joint were in excess of 200% of both the displacement and stress on vertebrae or discs [9]. Regarding implant performance, Kettler et al. investigated the wear rates of Prodisc-L devices tested under ISO 18192-1 (Wear of total intervertebral spinal disc prostheses -- Part 1: Loading and displacement parameters for wear testing and corresponding environmental conditions for test) and found that testing at 2Hz resulted in increased wear as compared to the traditional 1Hz testing rate [10].

Several studies have concluded that the resonance frequency of the spine is approximately 5Hz. [6,11,12]. While dynamic evaluations of elevated frequency effects have been conducted few have examined loading frequencies in excess of the resonance frequency [8]. One drawback to whole body vibration is identifying the exact frequency and magnitude of load applied to structures of interest. Through cyclic loading at these elevated frequencies, one may investigate the temporal effects of elevated frequency loading. Furthermore, using this temporal data, extrapolation to prolonged exposure is possible, though it should be noted that under these in-vitro conditions, one must also give some credence to specimen degradation as well as the lack of physiological repair.

In this paper the investigators applied cyclic compression to spinal facet joints over a range of loading frequencies from the physiologically accepted value of 1Hz to a high rate of 80Hz so as to span frequencies encountered under occupational exposure. We hypothesized that elevated frequency loading changes the mechanical response of the facet joint to loading. In doing so, the results indicated that elevated loading frequencies stiffened the facet joint and indicated a continuous accumulation of strain at frequencies beyond 1 Hz. These findings are mechanical evidence toward a predisposition of those individuals associated with high frequency occupational exposure for increased incidence of low back pain.

2. Materials and Methods

Facet joints from six 100kg bovine L4-L5 vertebral bodies (Animal Technologies Inc., Tyler, TX) were embedded in resin and secured to a mechanism that permitted translation and rotation in the X-Y plane to allow perpendicular alignment of the test surface to the loading axis. Each loading site was subjected to 520 loading cycles from -15N (19MPa) to -60N (76MPa) using a 1mm diameter indentor (Figure 1).

Previous work has shown that continuous loading over extended cycles can lead to specimen degradation. These testing parameters are comparable to those cited by Zioupos et.al, where specimens under 80MPa were failing at approximately 550 cycles using human cortical bone [13]. Load versus deformation data was recorded at cycle 5 and at subsequent 25-cycle intervals. The central region of the facet was tested at 1Hz with surrounding sites at distances of 2 indentor diameters randomly subjected to loading frequencies of 5Hz, 20Hz, 40Hz and 80Hz [14]. The maximum deformation at each cycle interval was computed and averaged across all specimens for each frequency, initialized to zero at the initial cycle interval and plotted verses cycle number. The stiffness in the elastic region was computed by performing a linear regression for load versus deformation using data from the first complete loading cycle at each cycle count interval.

Stiffness data at each respective cycle count was subsequently averaged across all specimens for each frequency and plotted versus cycle number. For each frequency, the cycle strain was computed and averaged across frequencies for each cycle over all specimens. The cumulative strain versus cycle number data was also computed. All parameters were subjected to non-linear exponential regression. The resulting regression produced the parameters of Yo (initial net deformation), K (rate constant of net deformation change), Plateau (asymptotic limit of net deformation) and Span (Yo - Plateau) which were examined using a 1-way ANOVA with a Tukey post-hoc test for between frequency comparisons. The K values for maximum deformation were converted to half-life according to the relationship: half-life = ln2/K. Half-life in this context represents the number of cycles required to attain 50% of the asymptotic deformation limit or Plateau.

3. Results

Figure 2 depicts the net deformation versus cycle number at each frequency. All comparisons for Plateau values were statistically significant between frequencies. (P<0.005 all comparisons)

The resulting K value or rate of net deformation per unit cycle at elevated frequencies (>1Hz) displayed statistically significant decreases with respect to the 1Hz frequency (Figure 3).

No statistically significant differences between K values were detected between 5Hz and 40Hz or 80Hz. However the associated K value with the 20Hz frequency was significantly decreased as compared to the 5Hz frequency. The K value associated with the 20Hz frequency was significantly different as compared to 80Hz (P<0.05) but not 40Hz.

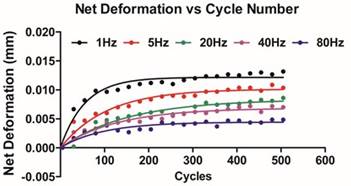
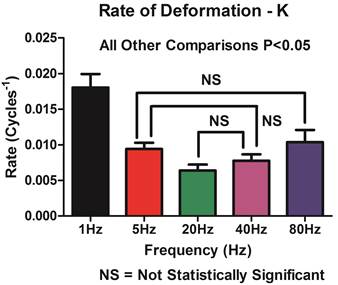
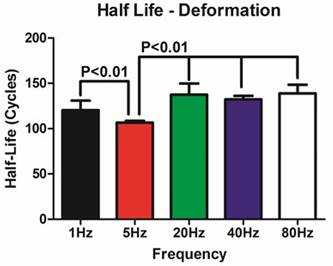
The asymptotic deformation values or Plateau achieved by the facet surface based on frequency were statistically significant. (P<0.005 all comparisons) All elevated frequencies (>1Hz) displayed statistically significant decreases with respect to K (P<0.05 over all comparisons). The half-life data for deformation indicates that the 5Hz is statistically decreased as compared to all other frequencies tested (Figure 4).

The regression results of stiffness versus cycle number also indicated an exponential relationship. Both the initial stiffness (Yo) and asymptotic limit of the stiffness (Plateau) increased as the frequency increased with all comparisons between frequencies statistically significant (P<0.05 for all). With respect to the Half-Life stiffness data, no statistically significant differences were found between the 5Hz and 20Hz, or the 1Hz and 80Hz frequencies. All other comparisons were statistically significant (P<0.05).

A decrease in the K value (that is, an increased number of cycles to obtain the asymptotic stiffness limit) was seen as the frequency increased from 1Hz to 40Hz. At the 80Hz loading frequency, the K value was comparable to that observed at the 1Hz loading rate.

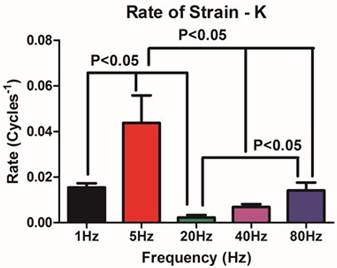
The cycle strain indicated that both the initial and asymptotic limit of the strain decreased with increasing frequency (P<0.05 for all comparisons). The K value for strain (or rate of strain change per cycle) indicated that the 1Hz loading frequency was statistically equivalent to both the 40Hz and 80Hz frequencies (P>0.05 for both) The 5Hz frequency K value was statistically increased as compared to all other frequencies (P<0.01 for all comparisons)(Figure 5).

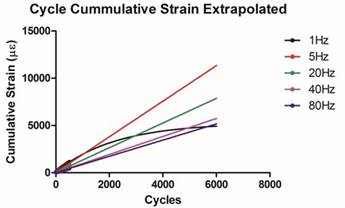
For the cumulative strain data, all frequencies above 1Hz displayed a linear response between strain accumulation and cycle number whereas at 1Hz frequency an exponential relationship was evident (P<0.001, F- test)(Figure 6). A statistical comparison of the linear regression slopes for the elevated frequencies versus the K value for the 1Hz frequency indicated that all elevated rates were statistically different as compared to 1Hz loading(P<0.001 for all).

4. Discussion

In a review of the literature concerning elevated frequency loading, Hill et al. determined that while studies displayed deficiencies, vibrations remain an important consideration in evaluation of patients presenting with discogenic back pain and that long term clinically controlled studies will be required for a definitive determination of vibrational effects upon spinal loading [15]. Determination of spinal resonance frequency is difficult as the frequency response is affected by multiple factors which include posture, seating, and inclination [6]. Despite variations in experimental methods, the resonance frequency of the spine has been cited between 5Hz and 12Hz with the greatest transmission occurring at the first resonant frequency of 5Hz [6,15].

At these elevated frequencies damping may result in considerable energy transfer. This was validated in this study by statistically increased values in initial and asymptotic stiffness values as loading frequency is elevated (Figure 7).

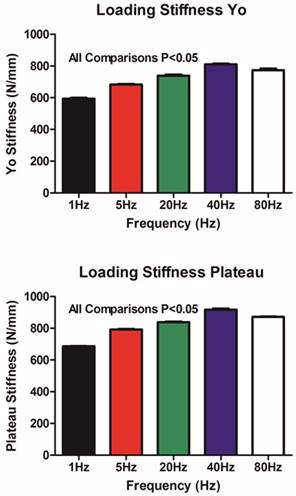
With increased frequency, increases in initial stiffness and cycles required to achieve stability (i.e. decreasing K values for stiffness) were seen. This is in keeping with the work by Wilder et al., where stiffening of the spine was reported in response to loading at increasing frequency. Further, it has been found that structures vibrated at the first resonant frequency have greater potential for damage [16]. In this study, a similar finding that 5Hz frequency loading was more often found to be associated with more detrimental mechanical parameters as compared to the other elevated frequencies.

In this study, the combination of decreasing K values (for deformation and stiffness respectively) and elevated initial stiffness may constitute a predisposition in individuals for the onset of facet joint degeneration. This is significant in that viscous damping may result in significant energy transfer. At elevated frequencies muscles become fatigued and require increased time to react to sudden loading thereby making the spine more susceptible to injury [6]. Guo et al. noted that whole body vibration of human spine is more dangerous to facets, which may lead to abnormal remodelling and degeneration of the lumbar spine [9].

Bone, as many viscoelastic tissues, increases in strength with strain rate. While the applied loading is uniform, the reduction in initial strain due to elevation in frequency results in an increased modulus or stiffening. The 40Hz and 80Hz frequencies may be acting as a low frequency or quasi-static condition in that the fluid flow within the tissue has achieved static equilibrium and hence the viscoelastic effects are comparable to those at low frequency.

The cumulative cycle strain data has clinical implications in that eventual attainment of a plateau level is attained at 1Hz while elevated frequencies continue accumulation indefinitely. If one considers the continued exposure of these elevated frequencies by extrapolating to several thousand cycles the evidence suggests dramatic and potentially detrimental conditions regarding the continued strain accumulation. As can be seen, the elevated frequencies quickly surpass the strain accumulation at the 1Hz frequency by a little as 6000 cycles or less than 2 hours (at 1Hz).

This study indicates that increased strain accumulation can occur at elevated loading frequencies over prolonged time periods and do so indefinitely at elevated frequencies. Patients exposed to occupational vibrations in the 4Hz to 20Hz range experience low back pain rates twice that of non-exposed patients. Clinically, the mechanical response of the facet joints is dependent on a variety of specific loading parameters that include loading magnitude, duration and frequency and as a result low back pain is a multifaceted condition and cannot be attributed to a single factor. However, to minimize overall exposure, one must reduce amplitude, dampen frequency and reduce time. These parameters will all play a role in the overall exposure reduction. To that end, these effects can be reduced through improvements in seat materials, and damping or suspension mechanisms [16].

5. Conclusions

This study demonstrates that increased stiffness at elevated loading frequencies is manifested and may be an indicator of low back pain propensity. This study presents a mechanical representation of the facet joint response to high frequency vibration conditions and may be a basis for determination of low back pain predisposition. Further, subsequent reduction or damping of these elevated frequencies may aid in clinical care of those under continuous exposure.

References